이제 아이들은 표준화된 세로셈 방법으로 덧셈과 뺄셈을 할 수 있습니다. 그런데 교과서에서는 또 다른 방법을 요구하지요. 이미 해결한 문제를 또 다른 방법으로 해결하라고 하니 귀찮고 어려울 수밖에 없습니다.
덧셈과 뺄셈의 다양한 풀이 방법 찾기
① 각자 편한 풀이 방법을 선택
② 아이들끼리 의사소통을 통해 자신의
풀이 방법을 설명
③ 또 다른 풀이 방법은 없는지 생각
여러가지 방법으로 연산 문제를 해결하는 것은 아이들의 다양한 사고에 중요한 영향을 미칩니다. 어려서부터 여러 가지 방법으로 문제를 해결하는 습관을 지녀야 나중에 문제를 다양한 관점에서 생각할 수 있어요. 나아가 자신이 알고 있는 방법으로
해결되지 않는 문제를 다른 각도로 바라보는
사고가 가능해집니다.
그런데 덧셈, 뺄셈과 같은 문제에도 여러가지 풀이 방법이 있을까요?
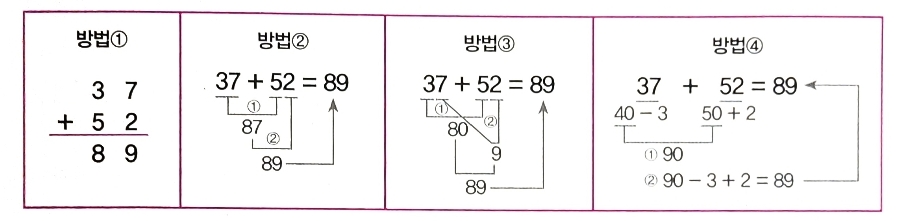
아이들이 가장 많이 이용하는 방법은 아마도 방법
1번일 것입니다. 방법 2번은 37에 50을 먼저 더한 후, 나중에 2를 더하는 방법입니다. 아이들이 머릿속으로 계산할 때 가장 많이 사용하는 방법이지요.
방법 3번은 십의 자리 수를 먼저 더한 후, 여기에 일의 자리 수끼리 더한 값을 합하는 방법입니다.
방법 4번은 37에 가까운 수인 40과 52에 가까운 수인 50을 먼저 더한 후, 3을 빼고 2를 더하는 방법이지요.
이번에는 뺄셈은 어떤방법이 있을까요?
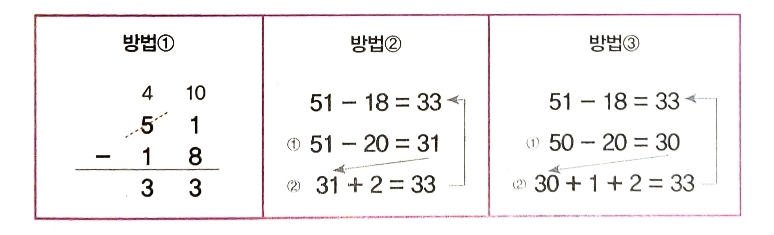
방법 1번은 아이들이 가장 많이 이용하는 방법입니다. 방법 2번은 18에 가까운 20을 뺀 후, 51에서 빼고 더 뺀 2를 나중에 더했습니다
방법 3번은 51에 가까운 50에서 18에 가까운 20을 뺀 후 1과2를 차례로 더했습니다.
실생활에서 덧셈과 뺄셈을 가장 많이 이용하는
경우는 아무래도 돈을 계산할 때입니다.
이때 우리는 종이와 연필로 계산하기보다 보통 머릿속으로 계산합니다. 정확한 계산이 필요할때도 있지만 어림하여 계산하는 경우도 많이 있습니다.
예를 들어 10,000원으로 1,800원짜리 아이스크림과 2,100원짜리 라면, 3,200원짜리 과일을 살 수 있을지 계산하려면 1,800원을 2,000원으로, 2,100원을 2,000원으로, 3,200원을 3,000원으로 어림합니다. 그래서 7,000원 정도 나올 것으로 예상하지요.
아이들도 점차 어림하여 계산해야 하는 경우를 경험하게 될 것입니다.
아이들은 언제 어림하는 경험을 할까요?
첫째, 미래에 대한 예측 또는 과거에 대한 추측과 같은 상황입니다. 값이 정확히 알려져 있는 것이 아니기 때문에 이때는 어림이 필요합니다.
둘째, 알고자 하는 값이 측정할 때마다 변하는 경우입니다. 예를 들면, 온도, 인구, 타자 속도 등을 나타내는 경우입니다.
셋째, 측정 기구가 정확하지 않을 때도 어림값이 필요합니다. 예를 들어, 몸무게를 재는 경우 kg에만 눈금이 있으면 kg보다 적은 양은 어림을 하여
표현해야 합니다.
넷째, 어떤 값이 자연수로 표현되기 힘든 경우에 어림값이 필요합니다. 예를 들어, 귤이 3개에 1,000원이라고 하면 귤 1개 값은 330원이라고 어림하는 경우나 6학년에서 배우는 내용 중
원주율을 구하는 경우 등이 여기에 해당됩니다.
마지막으로 17.9 × 4.1과 같은 연산에서 17.9 x 4.1을 18 × 4로 바꾸어 어림하는 경우가 있습니다. 이때는 정확한 값보다 계산의 편리성 때문에 어림값을 사용하는 것입니다.
!!친구들이 궁금해요!!
Q_가로로 계산하는 것과 세로로 계산하는 것은 다른방법인가요?
네, 물론입니다. 가로로 계산할 때는 받아올림과 받아내림을 머릿속으로생각하며 연산하지만, 세로로 계산할 때는 받아올림과 받아내림을 써가며
계산합니다. 둘은 서로 다른 방법이라고 할 수 있어요.
아이가 연산을 할 때 다양한 방법을 찾으려고 노력하는 것은 좋은 시도입니다. 가로셈이 세로셈에 비해 다소 불편하기는 하지만 머리를 많이 사용한다는 점에서 효과는 더 클 것입니다.
Q_다양한 방법으로 풀어야 하는 이유가 무엇인가요?
지금까지 수학 공부는 지식을 익히고, 계산 기능을 향상시키는데 많은 활동을 했어요. 그러나 수학은 논리적, 창의적 사고력을 키우기 위한 교과이기 때문에 최근 수학교육은 수학을 통해 실생활의 문제를 해결하고, 창의적 사고력을 키우는 데 중점을 두고 있습니다. 따라서 계산 방법에 의한 1가지 방법으로 문제를 풀기보다 자신만의 방법을 찾아 다양하게 풀어 보는 경험이 중요합니다. 자신의 방법을 발견하고 인정받게 되면 자존감을 키우는 데도 도움이 됩니다.
다만 1가지 문제를 반드시 여러 가지 방법으로 풀어야 하는 것은 아닙니다.각자 편리한 방법을 선택하여 문제를 해결하면 됩니다.